OpenGL Basics (3): Mathematical Foundations Ctn.

type

status

date

slug

summary

Local and World Space

When building a 3D model of an object, it's essential to orient the model in the most natural and intuitive way for describing it. For instance, when modeling a sphere, we would ideally position the sphere's center at the origin (0,0,0) and give it a convenient radius, such as 1. The space in which this single sphere model is defined is known as its local or model space.

In many cases, a 3D object may be part of a more extensive model or scene, such as a sphere being used as the head of a robot. In this scenario, the robot would have its own local space. To position the sphere model within the robot's model space, we can use matrix transformations for scale, rotation, and translation. This process allows for the construction of complex models in a hierarchical and recursive manner.

Now, let's consider the game world as a giant model containing all other models. In this context, we can define the position and orientation of a model within the game world using the same matrix transformation methods. The matrix responsible for positioning and orienting an object into world space is called a model transformation matrix.

Eye Space and the Synthetic Camera

The ultimate goal of 3D graphics rendering is to display a portion of the 3D space on a 2D monitor. Just as we can see the real world through our eyes from a specific point and direction, we can set up a virtual camera to "see" the 3D world. This virtual camera is known as the view space or synthetic camera.

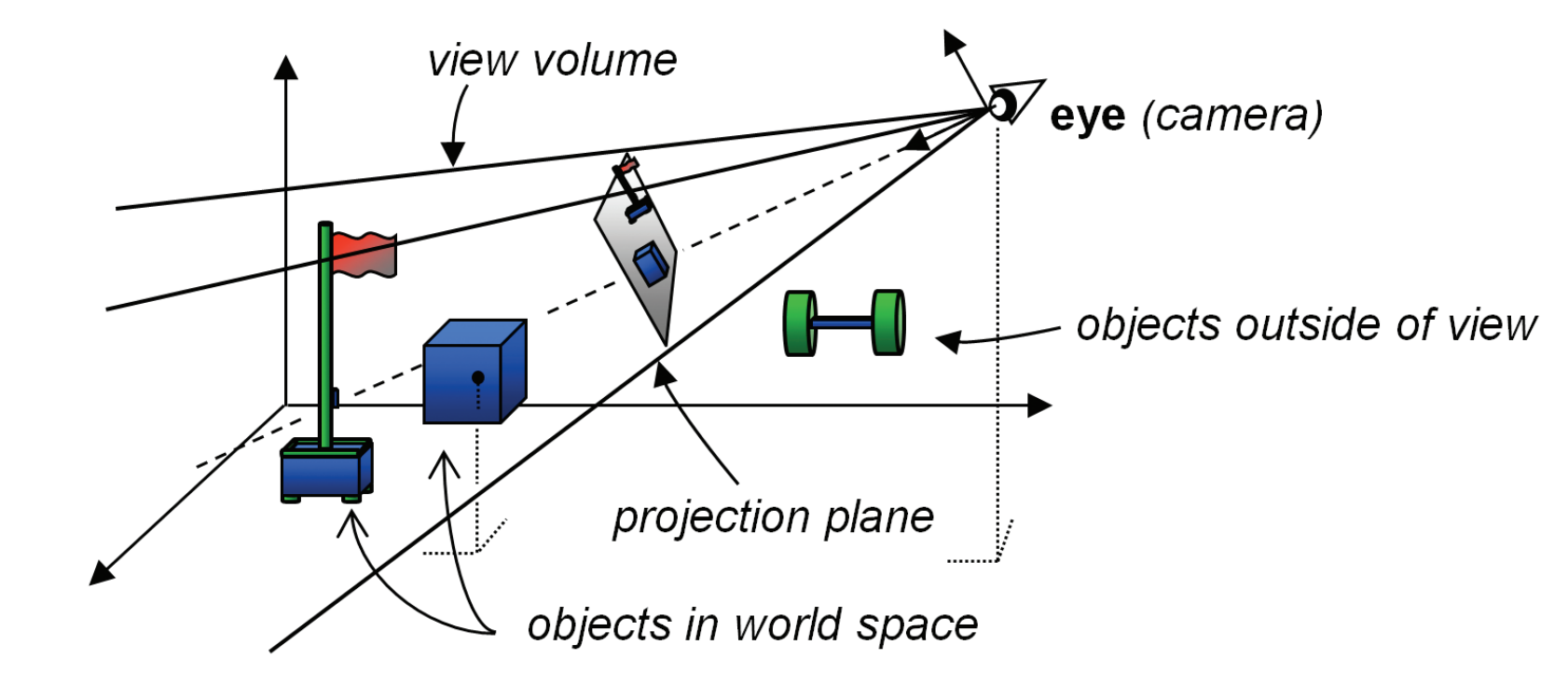
To render the 3D world with the synthetic camera, several steps must be taken:

Place the camera at a specific location in the world.

Orient the camera to face the desired direction.

Define a view volume to determine how much of the 3D world the camera can see.

Project the objects within the view volume onto a projection plane.

In OpenGL, a camera is permanently fixed at the origin and faces down the negative Z-axis.

However, to create a more immersive experience, we often want to view the 3D world from different angles and locations. To achieve this, we simulate moving the camera to the desired location and orientation by actually moving the objects instead of the camera itself. The position and orientation of the camera always remain fixed in OpenGL.

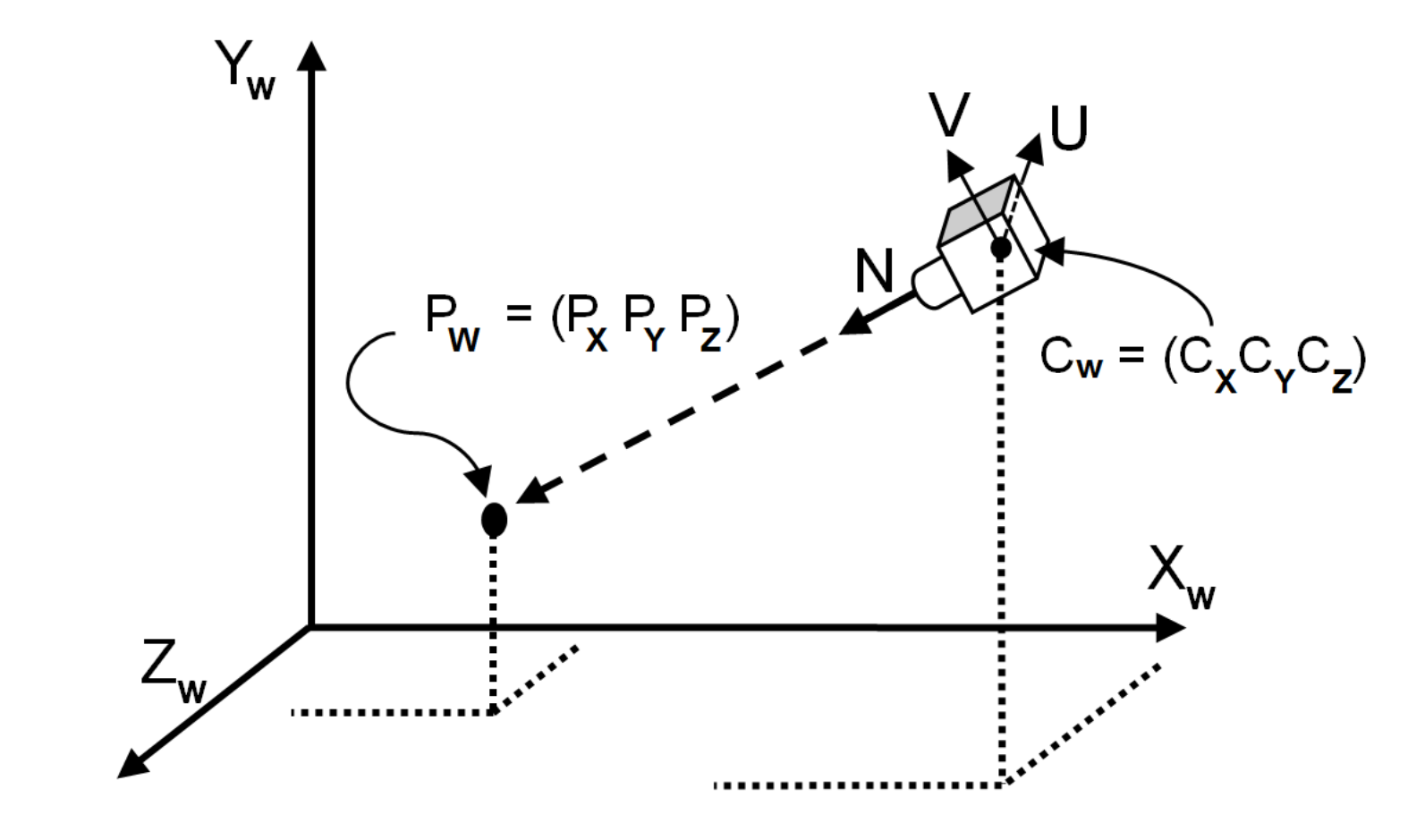
Assuming a point at world space location and a simulated camera at desired position looking directly at , we need to represent Pw in the space where is the origin. This can be done by translating by the negative of the desired camera location and rotating by the negative of the desired camera orientation Euler angles. We can combine these steps into a single transformation matrix called the viewing transform matrix.

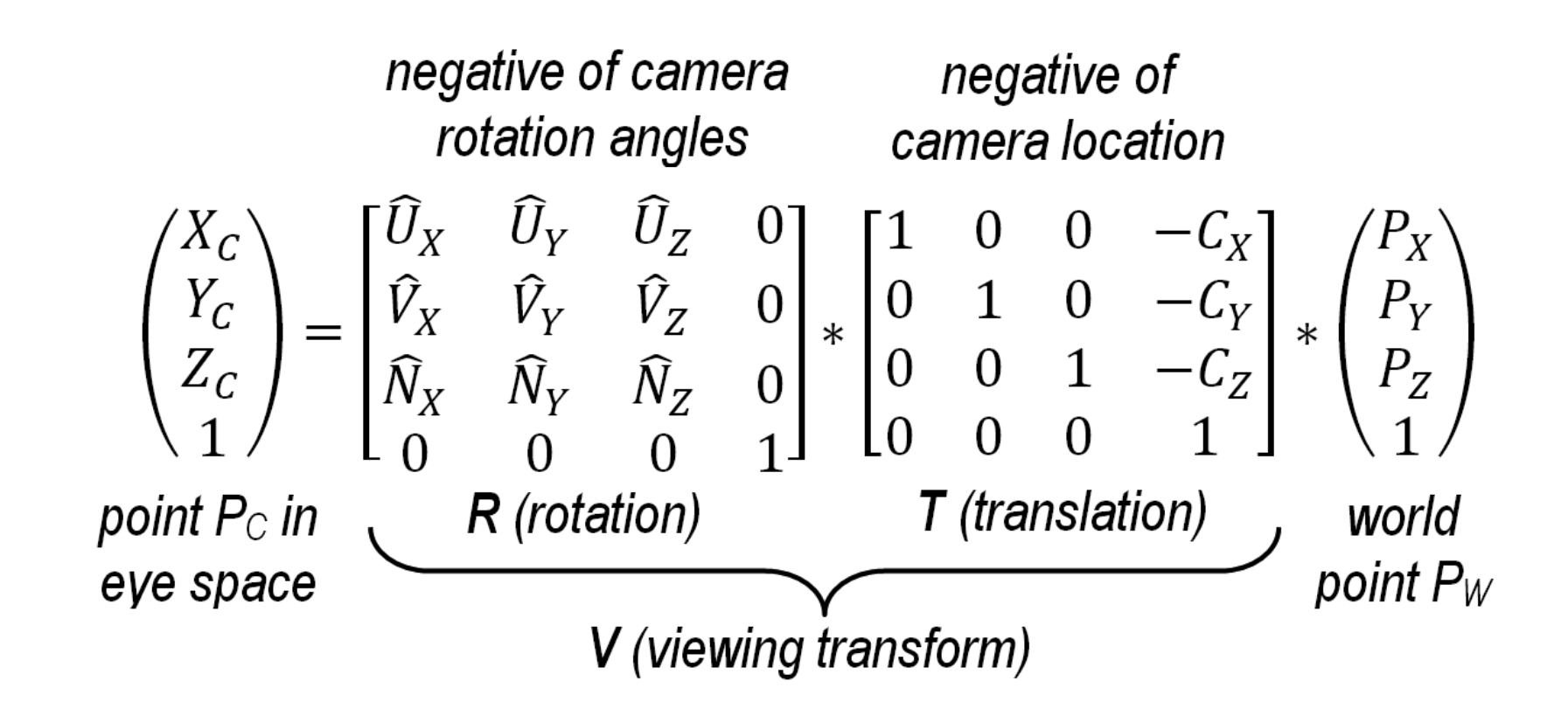
It's also common to combine the view transformation matrix (V) and the model transformation matrix (M) to form a single model-view transformation matrix (MV).

Projection Space

Now that we have established the camera and found a way to represent every single point in every model within the camera space, it's time to examine the projection matrices. Two important projection matrices are the orthographic projection and the perspective projection. To briefly explain the difference, orthographic projection represents objects with parallel projection lines, maintaining their true size and shape, whereas perspective projection uses converging projection lines to create the illusion of depth and distance, similar to what we perceive with our human eyes in real life.

Perspective Projection Matrix

With perspective projection, objects that are closer appear larger than those further away. Additionally, lines that are parallel in 3D space no longer appear parallel when drawn with perspective. In order to find a transformation matrix that achieves perspective projection, we need to define the four parameters of a view volume, or frustum: aspect ratio, field of view, near clipping plane, and far clipping plane.

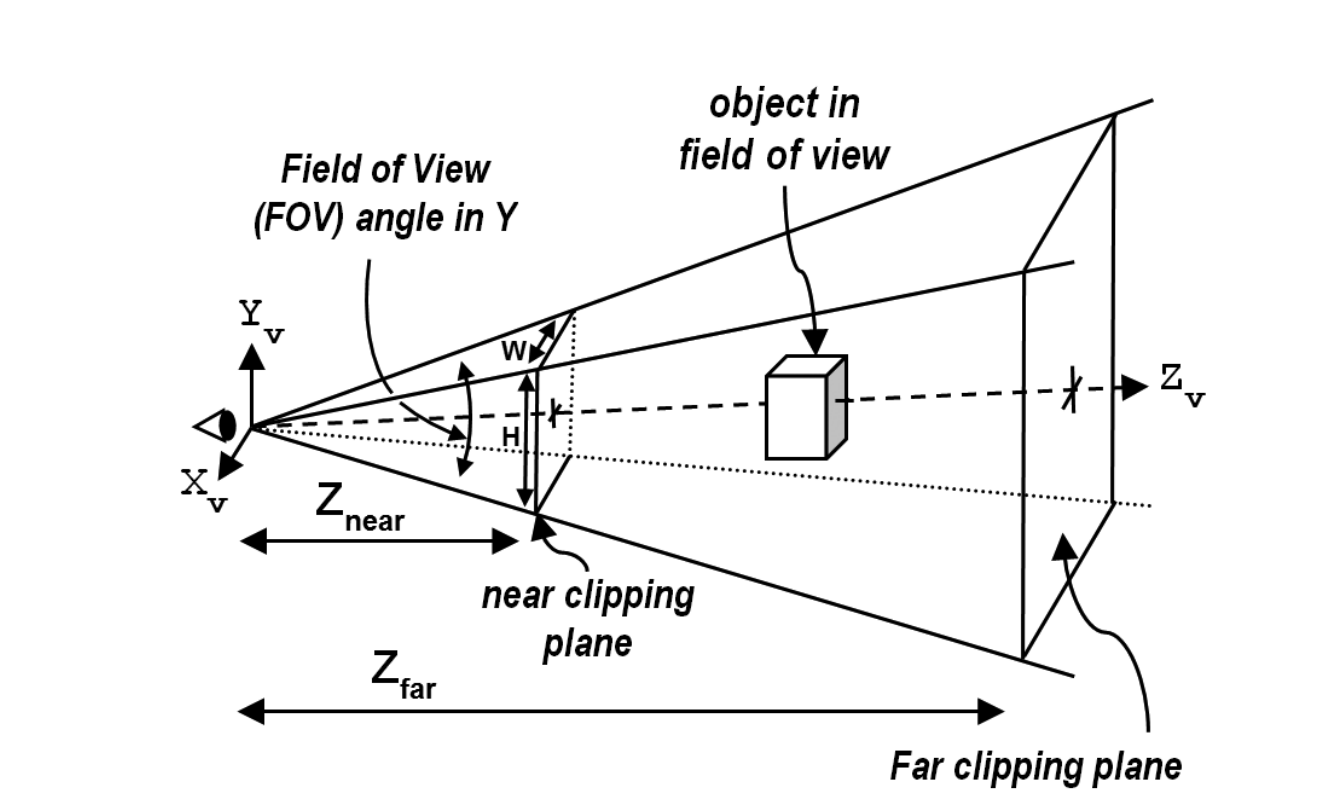
The shape formed by these four elements is called a frustum. The field of view (FOV) is the vertical angle of the viewable space, and the aspect ratio is the ratio of width to height in the near and far planes. Only objects inside the frustum and between the near and far spaces are rendered.

The near plane serves as the plane on which objects are projected. Generally, it is positioned close to the eye or camera. In OpenGL, this means it has a higher z value than the far plane, as the camera always faces the -z axis. The perspective projection matrix takes all the frustum parameters into consideration and transforms points in 3D space to their appropriate position on the near clipping plane. The GLM library includes a function glm::perspective() for building a perspective matrix, or you can find the formula online to manually build one yourself.

Orthographic Projection Matrix

In orthographic projection, parallel lines remain parallel. Objects within the view volume are projected to the near plane directly, without any adjustment of their distances from the camera. To find a transformation matrix that achieves perspective projection, we need to define the parameters of a view volume, or frustum: the near plane , the far plane , and the coordinates of the boundaries of the projection plane . Similarly, the GLM library includes a function glm::ortho() for building a orthographic projection matrix, or you can find the formula online to manually build one yourself.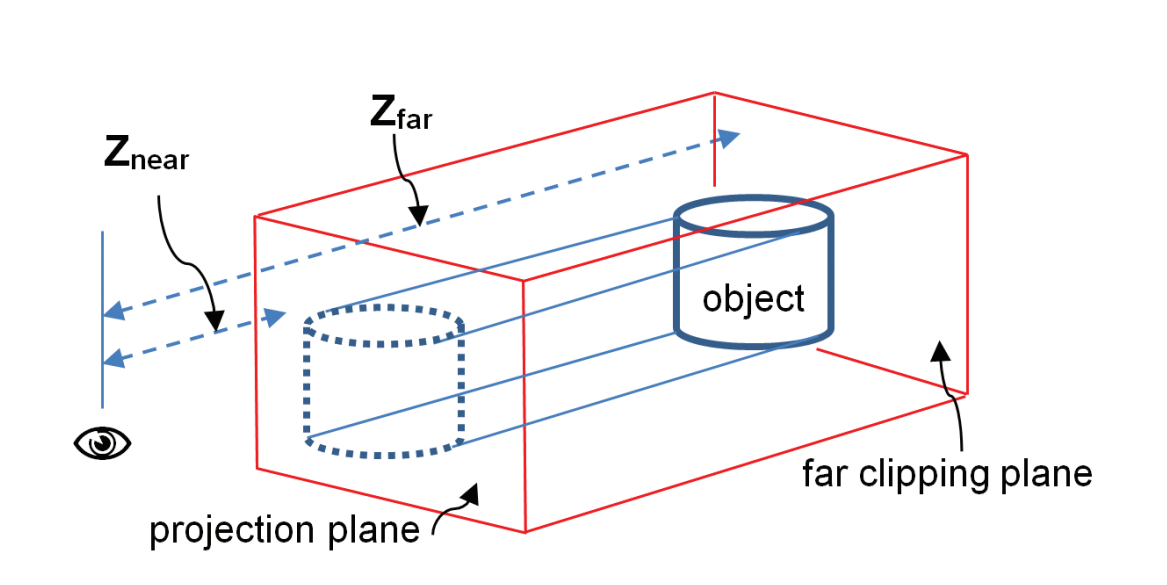

Look-At Matrix

The look-at matrix is an incredibly useful tool when we want to position a camera at one location and have it look towards a specific point. It's important to remember that the camera itself is fixed; our actual goal is to translate and rotate the object so it appears as though the camera is viewing it from a certain angle and distance.

To define the look-at matrix, we first need to determine a few essential vectors: the forward vector, the up vector, and the right vector.

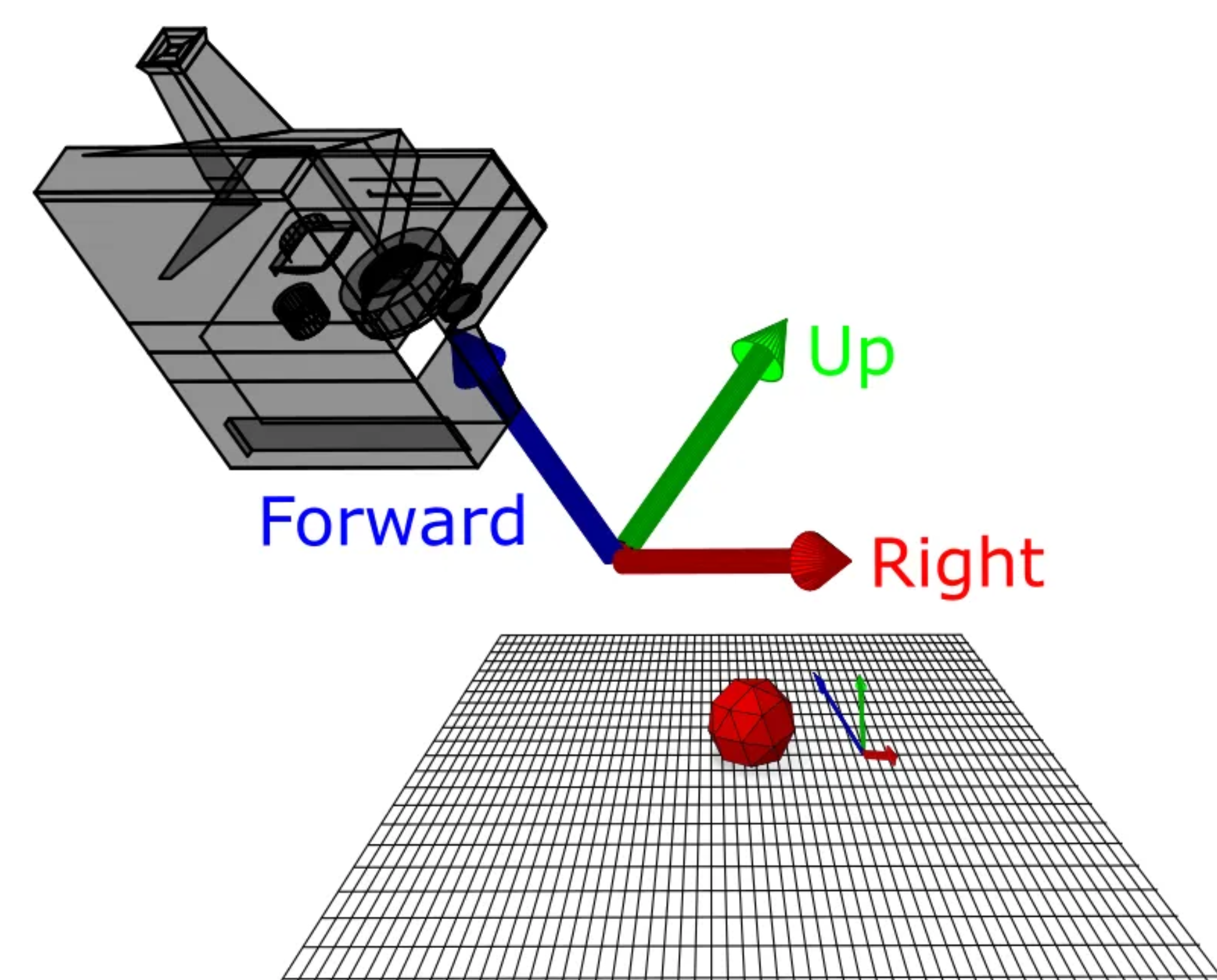
Calculating the Forward Vector

This is a straightforward process. Given our camera position and the position of the object we want to look at, we can calculate the direction of the forward vector through vector subtraction:

Calculating the Right Vector

This step is a bit more complex. Let's first establish a few key facts:

We are reconstructing an orthonormal 3D coordinate system based on the position and rotation of our camera.

The right axis we seek is orthogonal to both the forward and up axes.

Now, we can conclude that the right axis is simply the cross product of the forward and up axes. However, calculating the up vector remains a question. The trick is that we don't necessarily need the up vector itself; we just need any vector that lies in the same plane as the forward and up axes. A common choice is to use the Y-axis (0, 1, 0) as the up vector.

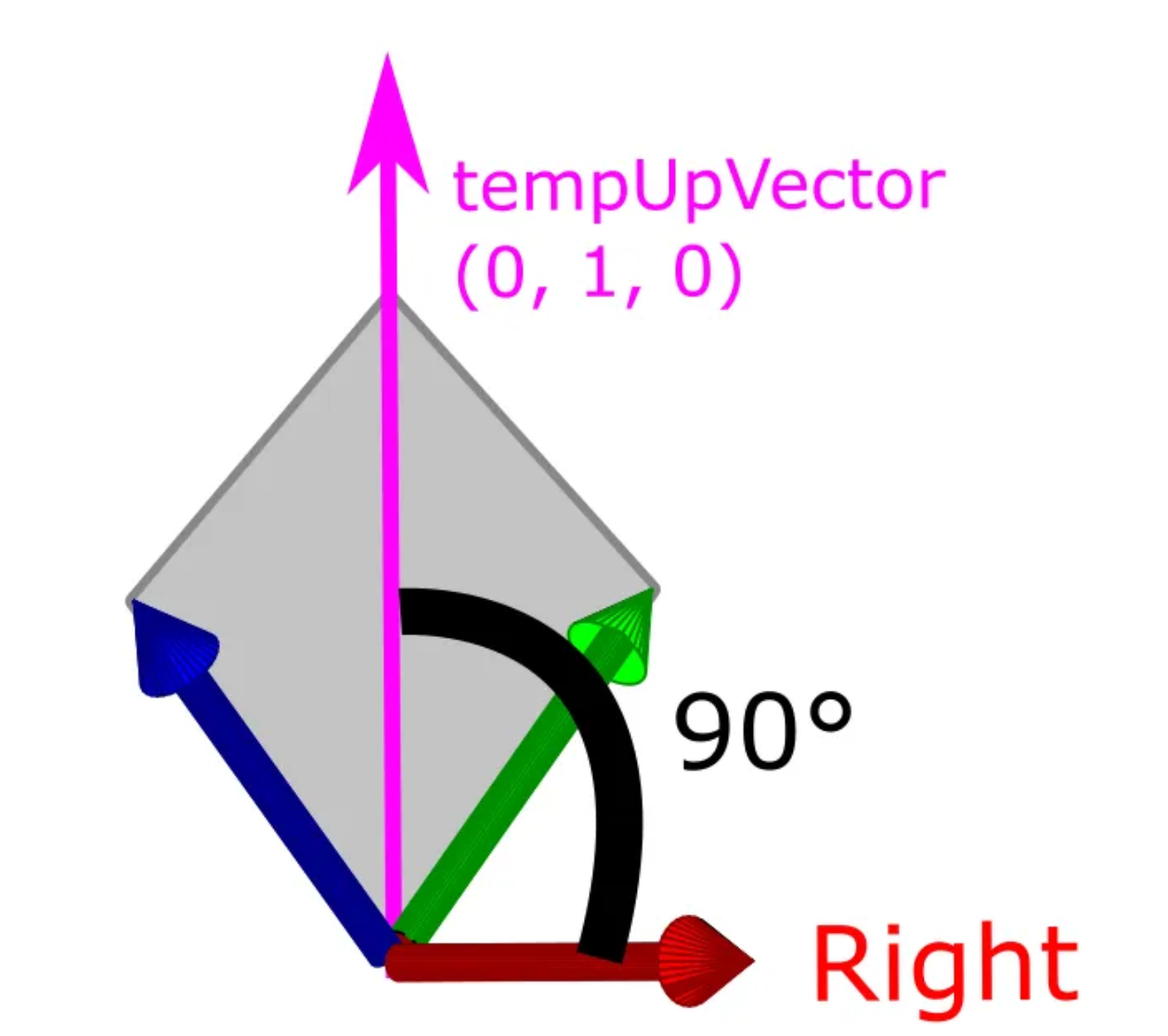
Therefore, we can compute the right vector as follows:

Calculating the Up Vector

Given the properties of the cross product, the up vector can be easily calculated as the cross product of the forward and right vectors:

Calculating the Translation Vector

Lastly, we need to determine how to translate our camera so it reaches the desired position in our coordinate system. It might seem logical to define our translation vector as the position of the camera. However, this is incorrect, as the coordinate basis has changed due to the rotation of our camera. To resolve this issue, we can simplify the operation by using the dot product:

Building the Matrix

With all of the vectors established, we can construct our look-at matrix by combining them:

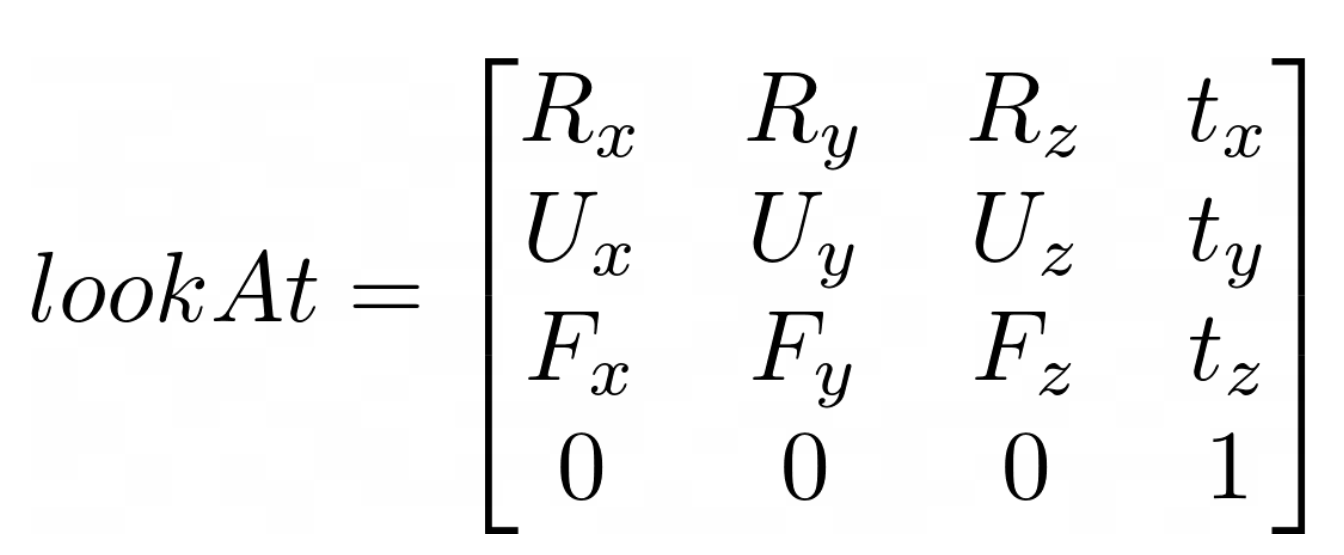
Now, we can create a simple C++ utility function that builds a look-at matrix given specified values for the camera location, target location, and the initial "up" vector Y.