OpenGL Basics (2): Mathematical Foundations

type

status

date

slug

summary

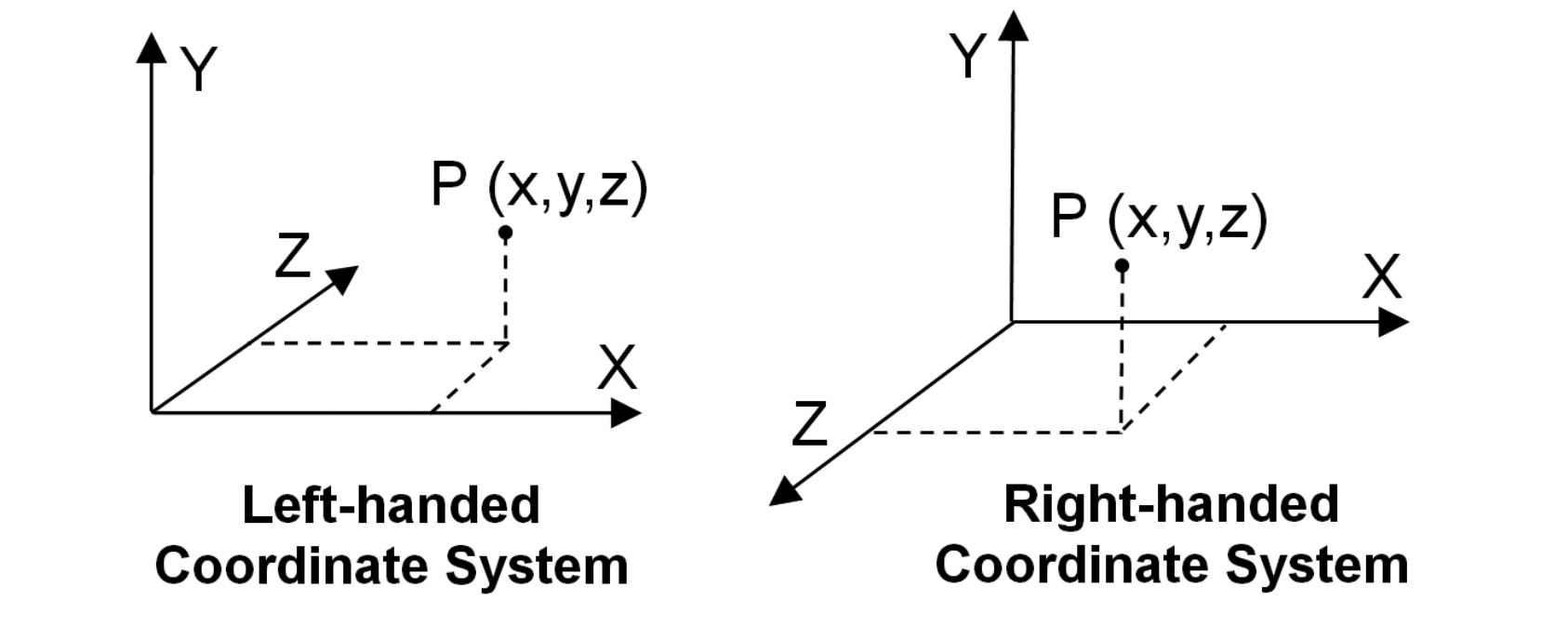
3D Coordinate System

A 3D coordinate system provides the basis for representing and manipulating objects in three-dimensional spaces. There are two main configurations for a 3D coordinate system: right-handed and left-handed. Most coordinate systems in OpenGL are right-handed, while DirectX primarily uses left-handed systems.

Points

Points in a 3D space can be specified using coordinates relative to the three basis axes . However, a more useful way to specify points is using homogeneous notation, which adds an extra value , usually set to 1. This notation allows for simpler and more efficient calculations, particularly when dealing with transformation matrices. In OpenGL's GLSL, the data type for storing points in homogeneous 3D notation is vec4.

This representation offers several advantages:

Simplification of Transformation Matrices: When using homogeneous coordinates, translation, scaling, and rotation can all be performed using matrix multiplication, which simplifies the calculation process (we will talk about this later).

Consistent Data Types: By using the same data type, like vec4, to represent both points and vectors, it becomes easier to write code that can handle both types of data without the need for explicit conversions.

Efficient GPU Operations: Representing points and vectors in the same way allows for efficient processing on the GPU, as both types can be stored in the same buffer and processed using the same shader code.

Vectors

Vectors represent magnitude and direction, and they are not bound to any specific location. In 3D graphics, vectors are often represented in the same way as points, with the vector being the distance and direction from the origin to the point. Many graphics systems, including GLSL and GLM, do not distinguish between points and vectors, using the data types vec3 and vec4 for both.

Dot Product

The dot product of two vectors is useful for various calculations, such as:

Finding the angle between two vectors

Determining a vector's magnitude

Checking whether two vectors are perpendicular or parallel

Checking whether two vectors are facing the same direction

Finding the minimum distance from a point to a plane

Cross Product

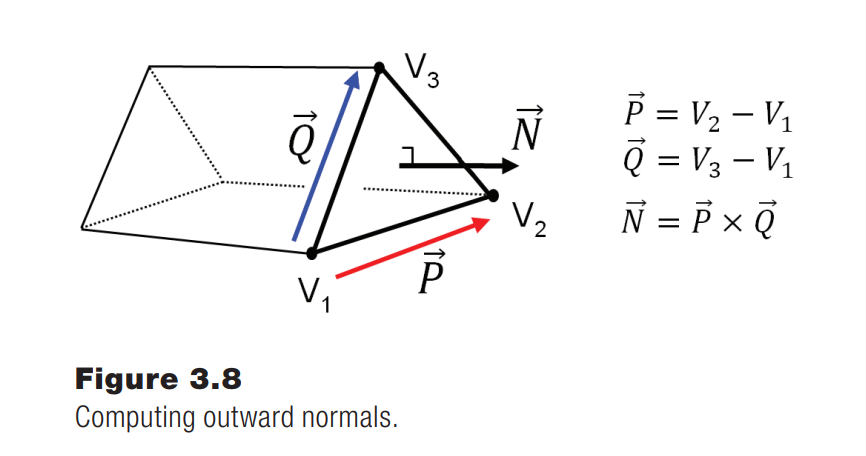
The cross product of two vectors produces a vector that is normal (perpendicular) to the plane defined by the original vectors. Any two non-collinear vectors define a plane, and the normal of that plane can be computed using the cross product. The direction of the resulting normal follows the right-hand rule.

The ability to find normal vectors using the cross product is extremely useful in calculating lighting. To determine certain lighting effects, we need to know the outward normals associated with the model being rendered.

Matrices & Transformations

Matrices are fundamental to 3D graphics computations, and most of them are 4x4 matrices. In OpenGL's GLSL and the GLM library, these matrices have the type mat4.

Transformation matrices are used to manipulate objects in 3D space. The main types of transformations are translation, scaling, and rotation.

Translation

Translation matrices move objects from one location to another. In the GLM library, a translation matrix can be created like this:

Multiplying a translation matrix with a homogeneous point results in a new point that has been moved by the translation values specified in the matrix.

Scaling

Scaling matrices are used to change the size of objects or move points towards or away from the origin. They can also be used to switch coordinate systems. In the GLM library, a scaling matrix can be created like this:

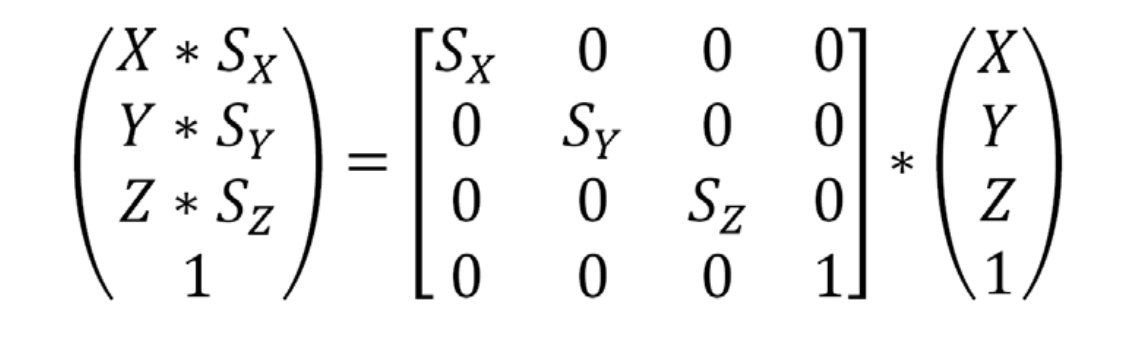
Rotation

Rotating an object in 3D space requires specifying an axis of rotation and a rotation amount (in degrees or radians). Conveniently, a rotation around any axis can be specified as a combination of rotations around the basis axes . These rotations are known as Euler angles, and they simplify the calculation of 3D rotation.

Euler Angle Rotation Formula

Most computer graphics math libraries, like GLM, provide built-in functions for creating rotation matrices based on Euler angles:

Euler Angle Artifacts

Despite their usefulness, Euler angles come with some limitations:

They suffer from singularities, which can cause instantaneous angle changes of up to 180 degrees.

They are inefficient for sequential rotations, as the rotation matrix must be recalculated completely.

They cannot be used to create smooth rotation animations, as linear interpolation between Euler angles is not possible.

Due to these limitations, quaternions are often preferred for computing rotations.

affine transformations

Up to now, we have seen two types of transformations:

Linear Transformations: These include scaling and rotation, which preserve collinearity and ratios of distances between points but may alter angles between lines.

Translations: These transformations involve moving points by a fixed vector, without changing the distance between them.

In essence, affine transformations can be thought of as a combination of linear transformations followed by a translation.

A 3-component vector cannot be used to perform affine transformations because affine transformations involve both translation and linear transformations. Linear transformations. To see why it is, consider the translation of a point in 3D space. Let's say we want to translate a point by a vector . We cannot represent the translation simply as a matrix multiplication with a 3-component vector because a 3-component vector only allows us to perform linear transformations, not translations.

One solution here is to represent a point as a 4-component vector , and a vector as a 4-component vector . We can then use a 4x4 matrix to represent the affine transformation, where the upper left 3x3 block corresponds to a linear transformation, and the last column corresponds to the translation vector.

To see how this works, Suppose we have a point and a vector . We want to perform an affine transformation that includes a translation of and a scaling of .

To perform this transformation using homogeneous coordinates, we first represent the point and vector as 4-component vectors by adding a homogeneous coordinate for the point and for the vector:

Next, we construct a 4x4 transformation matrix M that represents the desired affine transformation:

The upper left 3x3 block of the matrix corresponds to the scaling transformation, and the last column corresponds to the translation transformation.

To apply the affine transformation, we multiply the transformation matrix M by the homogeneous coordinates of the point and vector:

The resulting 4-component vector P'' represents the transformed point (7, 10, 13). Similarly, we can apply the same transformation to the vector V' by multiplying it by the transformation matrix M:

The resulting 4-component vector V'' represents the transformed vector (3, 4, 5), note the translation has no effect on the resulting vector, as vectors do not have positions.

Conclusion

Coordinate systems, transformation matrices, and vector operations form the basis for creating and manipulating objects in 3D space. In our next blog, we will start looking at different coordinate systems in OpenGL, and how OpenGL project the 3D world onto your 2D screen.